Recently on the subreddit for fantasy baseball, there was a thread about which stats you look at when trying to gain an edge over your league. A lot of the responses concerned pitchers, those most volatile of commodities and therefore the players who merit the most waiver-wire attention. The metrics most people cited as useful for pitchers were predictably strikeout-based: K/9, K%, K/BB.
Those stats are fine and useful in all sorts of situations, but I’m not convinced they really provide an edge. After all, if we suppose the people who post on the fantasy baseball subreddit are representative of serious fantasy players, it follows that the only edge K/9, K% and K/BB would provide is over casual players, the guys or gals who are there just to give the league enough members.
We must necessarily look deeper to find an edge over other serious players. Swinging-strike percentage (SwStr%) is deep! Instead of measuring strikeouts as a function of innings or plate appearances, it measures swinging strikes out of total swings. You can also call it Whiff% (Brooks Baseball does).
In the way of finding proof that SwStr% is great, I looked at all starting pitchers from the last decade (2004-2013) who had at least 50 IP in a season. That gave me like 1700 player-seasons, or near enough as makes no matter. TruStats from that badass data set after the musical break.
Fact: I am trying to rewrite that song for Jeremy Giambi.
First look how well SwStr% correlates with K%:

I meant Starting Pitchers, of course. Starter Pitchers are the three pitchers offered to you at the beginning of your franchise.
I wouldn’t have shown it to you if the correlation weren’t high, which .65 is. I would have instead felt ashamed that my hypothesis was wrong and kept the data forever secret. Then I would self-medicate. Smut peddlers of the world would rejoice.
Instead, intuition is borne out in the numbers. Whiffs beget strikeouts, perhaps more so than called strikes do. Now let’s see the difference between a whiff machine, an above-average whiff guy, etc. The following numerical endpoints are arbitrary, because whole numbers have that ancient allure which standard deviations lack. I like feeling connected to ancients. I’ll be an ancient someday and so will you.
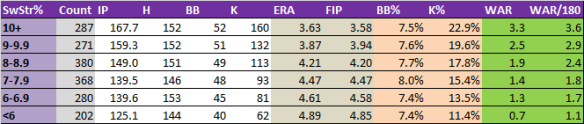
If the numbers look compressed, click to engorge. “Count” means how many pitchers fell into that group.
Pitchers with higher SwStr% pitch more innings with both lower ERA and FIP. Naturally, their K% exceeds their peers’ and their WAR is higher, partly because FanGraphs relies on FIP to calculate WAR. WAR/180 is just WAR prorated to 180 innings, a reasonable standard for the modern starter. Hits are unaffected, score another for DIPS theory. Walks are also largely constant; it seems that getting whiffs and avoiding walks are two distinct skills.
Finally (for today), here’s one big graphic showing the year-to-year correlation for four related stats. This dataset was a little smaller than the previous one of ~1700, because not every pitcher pitched two consecutive seasons of at least 50 innings. Here I have 1182 such pairs of player-seasons. You’ll definitely want to click to engorge.
I was mildly surprised to find K/9 had the most consistency between years. I would have guessed SwStr%, then K%. Anyway, SwStr% is right up there with the two foremost strikeout stats in terms of yearly predictability. But say you need a stat in the middle of a season to predict the next few months’ worth of games. I still think SwStr% would be the best there, because it has more data points. It’s a matter of pitches versus entire at-bats, and tomorrow I’ll see if this hunch is true.

